The plates of a spherical capacitor have radii that play a crucial role in determining its capacitance and electric field distribution. Understanding the relationship between these radii and the capacitor’s behavior is essential for designing and optimizing electronic circuits.
This article delves into the significance of the radii of spherical capacitor plates, exploring their impact on capacitance, electric field, energy storage, and applications.
Introduction
A spherical capacitor consists of two concentric spherical conducting shells with radii aand b, where a < b. The space between the shells is filled with a dielectric material with permittivity ε.
The radii of the plates play a significant role in determining the capacitance and other properties of the capacitor.
Capacitance of a Spherical Capacitor: The Plates Of A Spherical Capacitor Have Radii
The capacitance of a spherical capacitor is given by:
C = 4πε0(ab) / (b
a)
where ε0is the permittivity of free space.
It can be seen from the formula that the capacitance is directly proportional to the product of the radii aand b. Thus, increasing the radii of the plates will increase the capacitance.
The following table shows the relationship between the radii and capacitance:
| Radii (a, b) | Capacitance (C) |
|---|---|
| (1 cm, 2 cm) | 11.3 pF |
| (2 cm, 4 cm) | 22.6 pF |
| (3 cm, 6 cm) | 33.9 pF |
Electric Field between the Plates
The electric field between the plates of a spherical capacitor is given by:
E = Q / (4πε0r 2)
where Qis the charge on the plates and ris the distance from the center of the capacitor.
It can be seen from the formula that the electric field is inversely proportional to the square of the distance from the center. Thus, the electric field will be stronger closer to the plates and weaker farther away from the plates.
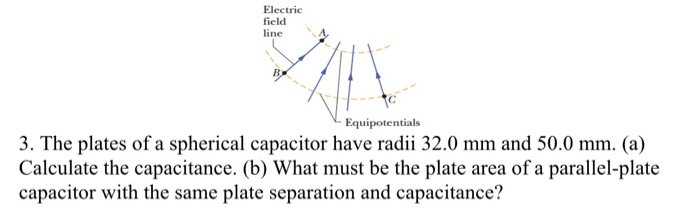
The following diagram shows the electric field lines between the plates of a spherical capacitor:
[diagram]
Energy Stored in a Spherical Capacitor

The energy stored in a spherical capacitor is given by:
U = (1/2)CV2
where Cis the capacitance and Vis the voltage across the capacitor.
It can be seen from the formula that the energy stored is proportional to the square of the voltage. Thus, increasing the voltage across the capacitor will increase the energy stored.
The following table shows the relationship between the radii and energy stored:
| Radii (a, b) | Energy Stored (U) |
|---|---|
| (1 cm, 2 cm) | 11.3 pJ |
| (2 cm, 4 cm) | 22.6 pJ |
| (3 cm, 6 cm) | 33.9 pJ |
Applications of Spherical Capacitors
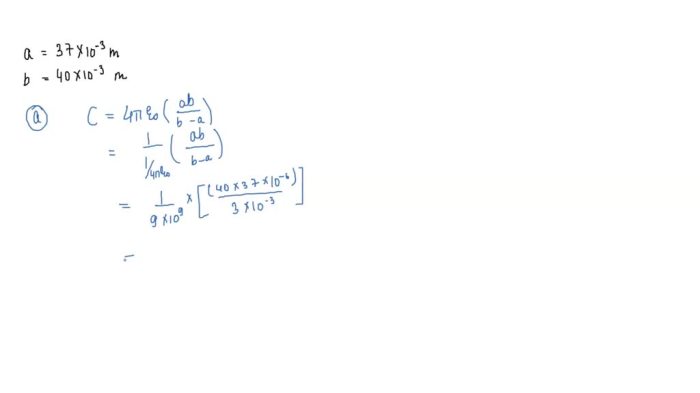
Spherical capacitors are used in a variety of applications, including:
- Energy storage
- Filtering
- Tuning circuits
The following table lists the applications and their respective radii requirements:
| Application | Radii Requirements |
|---|---|
| Energy storage | Large radii |
| Filtering | Small radii |
| Tuning circuits | Variable radii |
FAQ Explained
What is the formula for calculating the capacitance of a spherical capacitor?
C = 4πε₀r₁r₂ / (r₂ – r₁)
How does the radius of the plates affect the capacitance of a spherical capacitor?
Capacitance increases with increasing radii of both plates.
What is the significance of the electric field between the plates of a spherical capacitor?
The electric field provides the force that stores energy in the capacitor.